규칙
조건부의 지식을 표현하는 IF-THEN형태의 문장이다.
ex)
▷IF 연료통이 빈다 THEN 차가 멈춘다. // 인과관계
▷IF 여름철이다 AND 날이 흐리다 THEN 우산을 가지고 가라 // 추천
▷IF 차가 멈췄다 AND 연료통이 비었다 THEN 주유를 한다 // 지시
▷IF 차가 멈췄다 THEN 연료통을 확인한다 AND 단계1을 끝낸다 // 전략
IF 단계1이 끝났다 AND 연료통은 충분히 찼다
THEN 배터리를 확인한다 AND 단계2를 끝낸다
▷IF 시료가 액체이다 AND 시료의 PH가 6미만이다 AND 냄새가 시큼하다 // 휴리스틱
THEN 시료는 아세트산이다
Logic(로직)
Logic은 결론이 도출될 수 있도록 정보를 표현할 수 있는 형식적 언어이다.
Syntax는 문장의 문법이다.
Semantic은 문장의 의미이다. (True/False)
Entailment(함의)
Entailment 관계란 α가 β를 함의할 경우 β는 α의 결과를 따른다는 것입니다.
즉, α가 "true"이면 β도 "true"라는 것입니다. 이때 이때 α는 β의 subset 관계입니다.
α |= β ( "α entails β" or "β follows from α")
α가 β를 함의한다 = β는 α의 결과를 따른다
즉, 만약 α가 "true"이면 β도 "true"이다.
이때 α는 β의 subset 관계이다.
ex) α : 왕은 독살당했다 / β : 왕은 죽었다.
추론
KB ⊢i α 는 문장 α는 추론 절차 i에 의해 KB로부터 결과를 유도할 수 있다는 것입니다.
Soundness(건전성)
: 추론 절차 i가 sound하다는 것은, 만약 추론 절차 i를 통해 도출된 KB ⊢i α 가 True이면
α |= β 의 결과는 항상 True이다를 보장할 수 있는 것입니다.
Complementness(완전성)
: 추론 절차 i가 complet하다는 것은, 만약 α |= β가 True일 때 추론 절차 i를 통해
KB ⊢i α 의 모든 결과도 항상 True임을 보장할 수 있는 것이다.
논리적 동치 관계
두 가지 풀이 : 동치 관계 풀이, Truth Table
p → q ⇔ ¬p∨q
p → q ⇔ ¬q → ¬p
p∨q ⇔ ¬p → q
p∧q ⇔ ¬(p → ¬q)
(p → q) ∧ (p → r) ⇔ p → (q∧r)
(p → r) ∧ (q → r) ⇔ (p∨q) → r
(p → q) ∨ (q → r) ⇔ p → (q∨r)
(p → r) ∨ (q → r) ⇔ (p∧q) → r
유효, 만족 가능성
풀이 : Truth Table
명제논리 -
추론 규칙
: 추론 규칙은 우리가 가지고 있는 지식(KB)과 이미 알고 있는 사실로부터
새로운 사실을 유추해내는 것이다.
1) 전건긍정
: A가 True인 것으로 정의하면, B도 True라는 결론을 얻는 논리 규칙
규칙 | A → B
사실 | A
-----------------
결론 B
2) 부정논법
: 규칙의 결론이 False인 경우 해당 조건 또한 False로 추론하는 것
규칙 | A → B
사실 | NOT B
-----------------
결론 NOT A
3) AND조건의 삭제
: A가 True이며 A^B의 결론이 True인 경우, B 또한 True로 추론하는 것
규칙 | A ∧ B
사실 | A
-----------------
결론 B
4) 삼단논법
: 두 개의 규칙을 연쇄적으로 작용시켜 새로운 규칙을 도출해내는 추론 방법
규칙 | A → B
사실 | B → C
-----------------
결론 A → C
추론 규칙 이용한 증명



명제 논리 -
증명 방법
1) Forward Chaining (전방 연쇄/순방향 추론)
: 알려진 사실로부터 출발하여 결론을 이끌어내는 방법이다.
2) Backward Chaining (후방 연쇄/역방향 추론)
: 목표를 설정하고, 이를 증명하는 증거를 찾는 방법이다.
Forward Chaining (전방 연쇄/순방향 추론)
KB rules(지식베이스 규칙)
P ⇒ Q
L ∧ M ⇒ P
B ∧ L ⇒ M
A ∧ P ⇒ L
A ∧ B ⇒ L
사실(Fact(True))
A
B
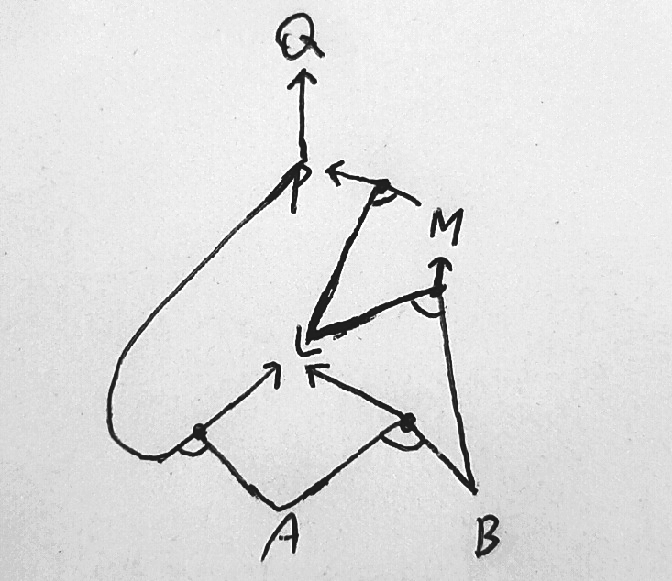
Forward Chaining vs. Backward Chaining
Forward Chaining은 Data-Driven 방법이다. 사실을 모은 후 이를 바탕으로 추론한다는 것이다.
Forward Chaining의 경우 목표와 관련없는 규칙들에 대해서도 살펴봐야한다. (BFS 방법과 유사)
Backward Chaining은 Goal-Driven 방법이다. 목표에서 시작하여 데이터들이 목표를 지원하는지 확인한다.
Backward Chaining의 경우 일반적으로 Forward Chaining보다 빠르지만(효과적),
완전성과 최적성을 보장하지 못한다. (DFS 방법과 유사)
명제 논리 -
CNF (논리곱 표준형)
명제 P와 명제 부정의 ¬P를 리터럴이라고 한다.
리터럴들이 논리합(∨)으로만 연결되거나, 논리곱(∧)으로 연결되면 절이라고 한다.
ex) P ∨ Q ∨ ¬R (논리합 절) , P ∧ Q ∧ ¬R (논리곱 절)
논리합 절들이 논리곱으로 연결되어 있으면 CNF라고 한다.
ex) (P ∨ Q ∨ ¬R) ∧ (¬Q ∨ R ∨ S) ∧ (P ∨ R ∨ S)
CNF 변환

연습문제 :
P ∧ (q → r) → p ∧ q
명제논리의 장단점
장점(Pros) :
명제논리는 문맥이 독립적이고 모호하지 않은 선언적 의미론을 기반으로 한다.
명제논리는 부분, 분리, 부정 정보를 허용한다.
명제논리는 구성적이다.
단점(Cons) :
명제논리는 표현력이 매우 제한적이다.
'전공 지식 정리 > 인공지능' 카테고리의 다른 글
| #7 머신러닝2 (0) | 2022.06.20 |
|---|---|
| #6,7 은닉 마르코프 모델, 머신러닝 (0) | 2022.06.20 |
| #4,5 불확실성 및 확률 / 베이지안 네트워크 (0) | 2022.06.19 |
| #2 문제해결 및 탐색 전략 (0) | 2022.04.23 |
| #1 인공지능 기술 동향 및 지능형 에이전트 (0) | 2022.04.23 |
